Inner defects visualization based on ultrasonic scanning

Abstract. Visualizing inner flaws and estimating their parameters (size, volume, orientation, type and so on) as a result of nondestructive ultrasonic testing is a problem of current importance in a field of modern flaw detection. Ultrasonic devices detect defect areas echoes and thus define volumetric defects as a set of points. This paper introduces a technique, based on Radial Basis Functions for building 3D defect model based on separate echo points. This model allows visualizing defect region, estimating its parameters and recognizing the type of flaw.

Introduction

Reliable inspection and estimation of inner flaws in a metal production (such as steel and cast iron rolls in metal manufacture) is a problem of current importance. Defective roll being used in a rolling workshop may result in crashes, stops of the mill and, thus, economical loss (Fig. 1). Current investigations have shown that inner flaws may have arbitrary three-dimensional topology that is proved by automatic ultrasonic scanning machines (Fig. 2). This paper introduces new, Radial Basis Functions based techniques for inner flaws computer modeling, visualizing and analysis. With a help of software, implemented using proposed algorithms an operator can timely inspect inner defects in full 3D and measure their parameters (volume, slices area, surface area) and thus prevent defective production from being used.

Figure 1. Defective broken roll

Overview

In this paper, inner flaw is considered to be a 3D object of arbitrary topology, defined with a set of points in 3D, produced by ultrasonic scanner. Such a definition of three dimensional solid shape is also known as point cloud surface or scattered data surface.

Figure 2. Demas Ltd. (Russian Federation) automatic ultrasonic roll-scanning system

Point cloud definition of 3D solid shape is not convenient for further visualizing and analysis. It can only be displayed on screen (or visualized) as discrete points without shading or depth effects (Fig. 3). The solution of simple analysis problems such as volume or surface area calculation is impossible or much complicated. It results in the need for designing 3D shape mathematical model free from above mentioned disadvantages.

Figure 3. Inner flaw representation as a result of automatic ultrasonic scanning

A vast volume of literature is devoted to the subject of scattered data reconstruction and interpolation. In most applications, Delaunay tessellation is used for 3D reconstruction. The main idea of Delaunay decomposition is to reconstruct a surface from non-uniform samples by connecting a subset of points that are natural neighbors in a triangulated mesh. This method applied in 3D builds a tetrahedral tessellation of scattered data, such that scattered points are vertices of neighboring tetrahedrons. A comprehensive overview of related studies, problems, and limitations [1] showed that Delaunay tessellation is a computationally complex problem and, moreover, produces not smooth model.

One other approach is to use methods of scattered data interpolation, based on minimum-energy properties [2], [3], [4]. These methods are widely discussed in mathematical literature ([5], [6]). One of the first attempts to automatically reconstruct implicit surfaces from unorganized point sets in 3D has been investigated by Muraki [7]. The reconstructed implicit surfaces were described by successive blending together several simple 3D base primitives minimizing an energy function.

The benefits of 3D surfaces modeling with the help of Radial Basis Functions (RBFs) have been recognized in [6] for Phobos reconstruction. RBFs were adapted for computer animation and medical applications [8], and were first applied to implicit surfaces by Savchenko [5]. However, the computational work required is proportional to the number of the grid nodes and the number of scattered data points. The amount of computation becomes significant, even for a moderate number of nodes. Special methods for reducing the processing time were developed for thin–plate splines [9]. Theoretical aspects of using radial functions in compact domains were discussed by Light in [10]. Carr have also recently worked on surface reconstruction of implicitly defined 3D objects based on the use of non–compact (fast) RBFs and a "both–side" approach, which has been proposed in [11]. Unfortunately, the authors of that paper did not describe their algorithm in detail. The approach taken by Turk and O’Brien in [11] of using points specified on both sides of the surface will provide successful restoration of a surface arbitrary topology, but it involves drawbacks that lead one to suppose that it would be inefficient for applying RBFs in volume reconstruction. It is beyond the scope of this paper to discuss all these matters; however, there is a problem of constructing or specifying off–surface points along a surface normal that also leads to a doubling of the given number of surface points. The "both–sides" approach also has a problem with surface extraction: a surface extractor can jump outside the band of non-zero points.

The main idea behind RBF-modeling is describing the whole solid shape with a single implicit function of three variables:

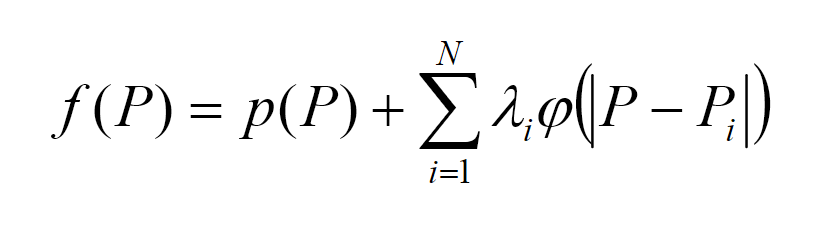
The function value is positive at points of three dimensional space outside the shape and is negative at those inside the shape. Zero level of RBF-model describes the surface. RBF-models, exploiting math behind implicit functions of several variables provide extended capabilities for analysis and visualizing freeform 3D shapes (Fig. 4).

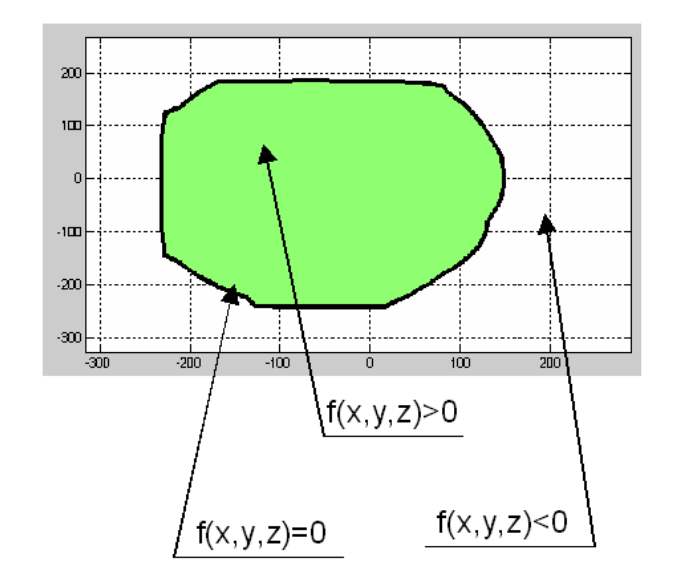
Figure 4. RBF behavior

Unlike many other modeling techniques RBF-modeling requires no prior knowledge about the shape being modeled and no prior knowledge about acquisition procedure (for instance, no information on scanning step or pathway is required whilst RBF-modeling).

Techniques

RBF-modeling is achieved via surface points interpolation, which in a turn produces the system of linear equations with matrix containing rows and columns number equal to the number of points. Attempts to commit interpolation directly lead to high computational complexity requiring supercomputing even for moderate points count (about thousands and more). Modern ultrasonic scanning systems (like Demas Ltd. one) are able to produce much more points (dozens of thousands per flaw), reflected from a flaw. So the design of optimization technique is of much importance. This work introduces new technique to optimize computational complexity at the stage before modeling, while modeling and after modeling while using RBF-model to analyze and visualize 3D inner flaws. New optimization technique is a result of combining several approaches.

First of all redundant points exclusion method should be applied to remove points at the areas of high density and low curvature of the surface. Incremental and hierarchical clustering and iterative simplification algorithms should be applied to create approximations of point-based models with lower sampling density. These methods work directly on the point cloud, requiring no intermediate tesselation. It can be shown how local variation estimation and quadric error metrics can be employed to diminish the approximation error and concentrate more samples in regions of high curvature [12].

Secondly RBF-centers reduction algorithm should be applied to remove those points which are redundant in a way the resulting surface would track them whether they present or not [13]. The same input data can be approximated to the desired accuracy using significantly fewer centers. A greedy algorithm is used to iteratively fit an RBF to the desired fitting accuracy. The greedy algorithm often results in a faster fitting time and smaller memory footprint, even with a moderate reduction in the number of centers.

And at last, basis functions at the compact domain should be used. Compactly supported RBFs (CSRBFs) are nonzero only at the finite definition domain, resulting in a special banded form of interpolation matrix [14]. CSRBFs are constructed from RBFs replacing basis function with the following:

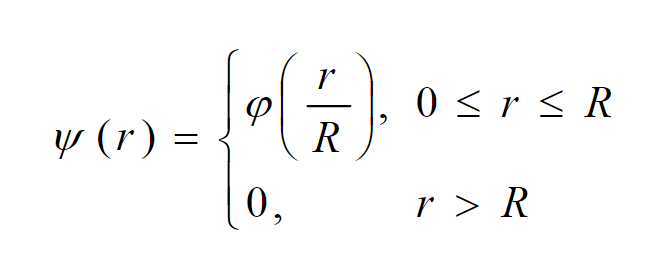
CSRBFs also greatly reduce number of items in a weighted sum of basis functions whilst calculation the value of RBF at some point of 3D space.

New optimization technique suggested here speeds up modeling process significantly and brings RBF-modeling problem from the field of supercomputing to the field of conventional computing.

To visualize RBF-modeled shape isosurface extraction algorithms is offered. In order to render the shape, a mesh representation of the shape is generated from the implicit function. This can be done using well known isosurfacing algorithms such as Marching Cubes or Marching Tetrahedra[8,9]. In these techniques, the isosurface localization is done by evaluating the function (which represents the surface) on a grid covering the objects space. This requires additional evaluations of the function in regions which doesn't contain any surface point. To overcome this problem and speed up the process, a new isosurface extraction algorithm is proposed. The main idea is to use the scattered points data themselves in order to localize the object surfaces, then evaluate, in the localized area, the RBF in order to get a more accurate localization. This approach speeds up the RBF evaluation considerably.

This work discovers 3D shapes geometry properties analysis using mathematical capabilities of radial basis implicit functions. The following geometric characteristics computation algorithms were designed. Volume of the shape can be computed as triple integral of unit function over the domain where RBF-model is negative (inside the boundary of the shape). This approach implies symbolic calculations which are too complicated and unclear to be implemented. That is why this work introduces algorithm based on numerical computations. The total volume is calculated as an arithmetical sum of elementary volumes of small cubes which fill the shape of interest. Surface area can also be theoretically defined symbolically, but this approach suffers from the above mentioned problems. So, surface area is computed as an arithmetical sum of areas of triangles generated by visualizing algorithm. 2D RBF-models of sections of the solid shape can be produced replacing the correspondent variable with a constant in an expression of implicit function describing RBF-model.

Conclusions

Methods described in this article were implemented as a part of Demas Ltd. automatic roll-scanning system (“RollScope”) and were applied at “Severstal” JSC (Russian Federation) NDT department. The developed software (Fig. 5) automatically visualizes, analyzes and explores flaws detected within a roll by automatic ultrasonic scanning system. This system reliably prevents defective rolls from being used.

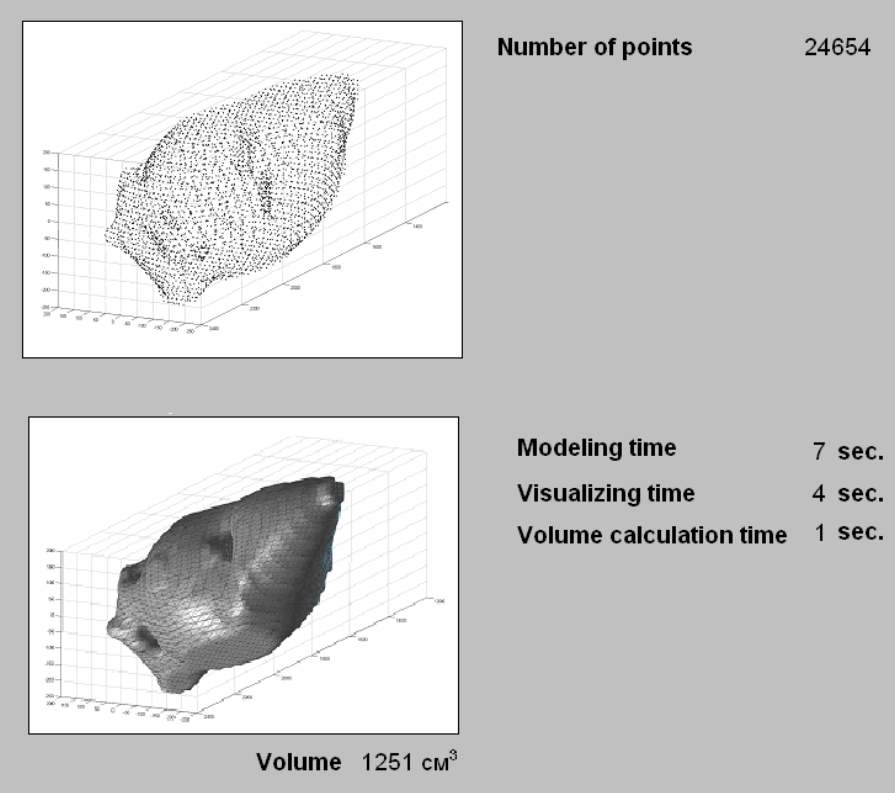
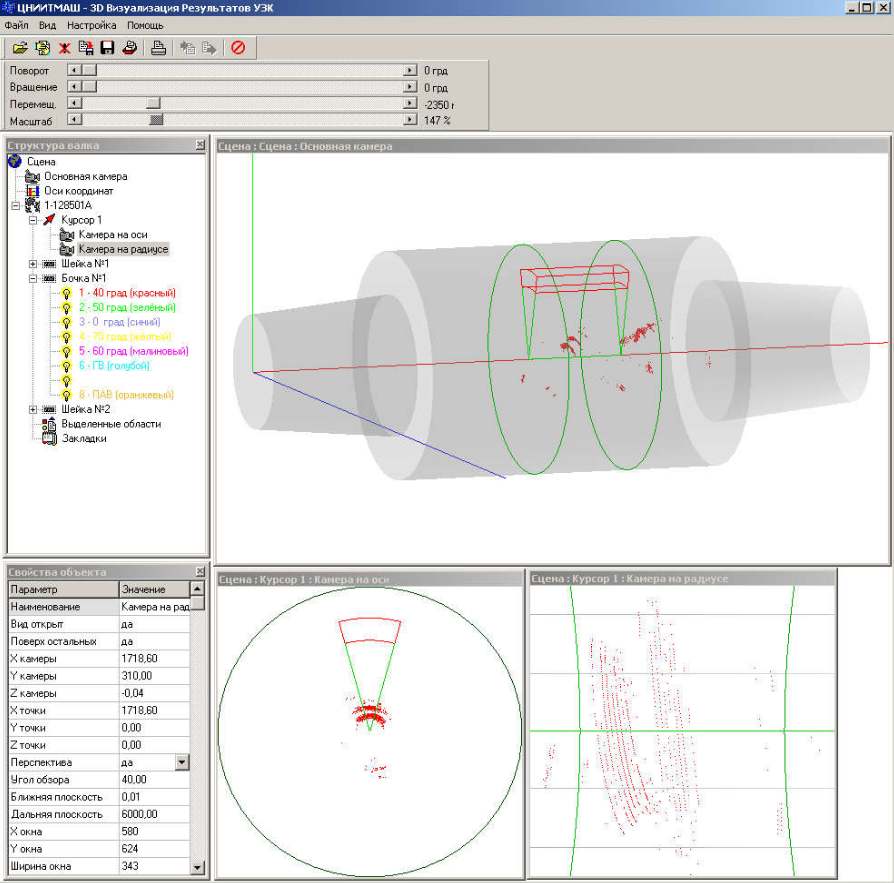
Figure 5. Screenshots of the software, showing roll and its inner flaws